Difference between revisions of "MainPage:Nuclear:Summer2012:RefractiveIndex"
| Line 12: | Line 12: | ||
We use a set-up with graph paper, a laser, aerogel, and measuring tools. The index of refraction can be measured using only the incident angle, the distance between the aerogel and a screen, and the amount the light is shifted on the screen after the aerogel is placed in front of the laser. | We use a set-up with graph paper, a laser, aerogel, and measuring tools. The index of refraction can be measured using only the incident angle, the distance between the aerogel and a screen, and the amount the light is shifted on the screen after the aerogel is placed in front of the laser. | ||
| − | + | [[File:aerogel.setup.jpg|thumb|center|320px|A picture of the index of refraction measurements. You can se the displacement of the laser by the aerogel]] | |
Revision as of 08:26, 11 July 2012
| ⇐ Back to Summer 2012 page |
| ⇐ Back to the Main_Page |
About Our Work
The index of refraction is a property of a material which dictates how quickly light travels through that material. As light passes through a material with one index of refraction to a material with a different index of refraction, the light changes speed and "bends" as it changes mediums. When light travels from a material with a low index of refraction to one with a high index of refraction, the light is bent toward the normal, and vice verse. We are working to measure the index of refraction of aerogel to a very high degree of precision. This value is significant because the aerogel will be used as a particle identification system in the Kaon Aerogel Detector at JLab to distinguish between Kaons and Protons according to their momentum.
Measurement Set-up
We use a set-up with graph paper, a laser, aerogel, and measuring tools. The index of refraction can be measured using only the incident angle, the distance between the aerogel and a screen, and the amount the light is shifted on the screen after the aerogel is placed in front of the laser.
The equation for calculating gamma based on the incident angle is ɣ = ɑ - (π/2) + arcsin[n•sin((π/2)-arcsin(sin(ɑ)/n))]
We can then use this equation to calculate the index of refraction; n = (sin2(ɑ) + cos2(ɣ - ɑ))½
Finding Error
We are finding lots of it...
Results
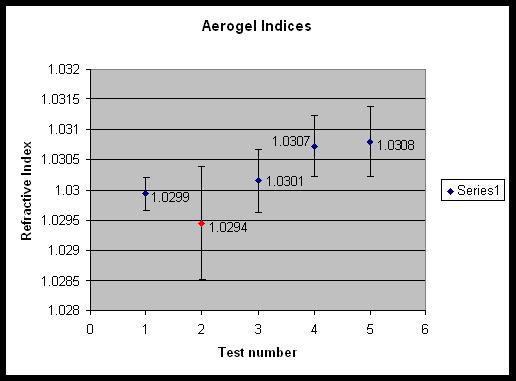
We have done several tests and all of them have fairly small error and are very close to the expected value, 1.03.
The average uncertainty in the above graph is 0.0005616, however we have not yet included uncertainty propagation in these results.