Difference between revisions of "MainPage:Nuclear:ChargeDistribution"
| (7 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
In this work we are going to calculate the transverse charge distribution of Pions. As a first step for this calculation, we are reproducing the Proton charge distribution from [http://arxiv.org/abs/1010.3629 Siddharth Venkat, 2010]. | In this work we are going to calculate the transverse charge distribution of Pions. As a first step for this calculation, we are reproducing the Proton charge distribution from [http://arxiv.org/abs/1010.3629 Siddharth Venkat, 2010]. | ||
| + | |||
| + | The equation: | ||
| + | <math> | ||
| + | \frac{1}{2} | ||
| + | </math> | ||
== Charged Pion Transverse Charge Distribution == | == Charged Pion Transverse Charge Distribution == | ||
| Line 19: | Line 24: | ||
{| border="0" style="text-align:center;" width="70%" | {| border="0" style="text-align:center;" width="70%" | ||
|- | |- | ||
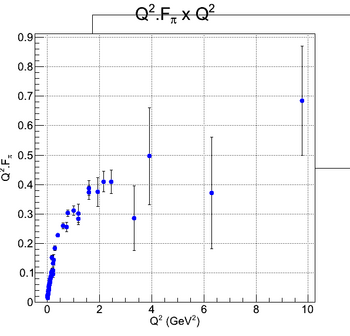
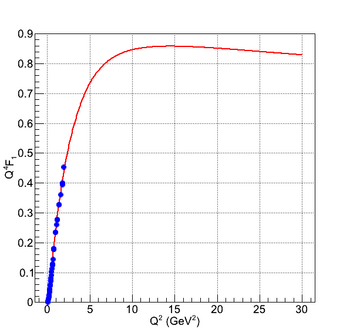
| − | | style="width: 50%;" | [[File:Pion_Q2F1.png|thumb|center|350px|Pion form factor. | + | | style="width: 50%;" | [[File:Pion_Q2F1.png|thumb|center|350px|Pion form factor.]] |
| | | | ||
|} | |} | ||
| Line 25: | Line 30: | ||
{| border="0" style="text-align:center;" width="70%" | {| border="0" style="text-align:center;" width="70%" | ||
|- | |- | ||
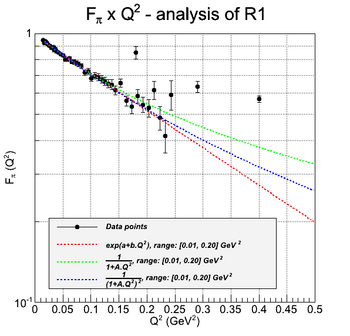
| − | | style="width: 50%;" | [[File:Pion_F1_RFit.png|thumb|center|350px| | + | | style="width: 50%;" | [[File:Pion_F1_RFit.png|thumb|center|350px|Fitting of the pion form factor for low Q^2, for finding its mean radius.]] |
| | | | ||
|} | |} | ||
| Line 31: | Line 36: | ||
{| border="0" style="text-align:center;" width="70%" | {| border="0" style="text-align:center;" width="70%" | ||
|- | |- | ||
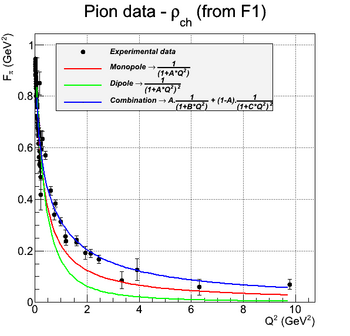
| − | | style="width: 50%;" | [[File:Pion_FF_Fitting.png|thumb|center|350px|Pion form factor. | + | | style="width: 50%;" | [[File:Pion_FF_Fitting.png|thumb|center|350px|Pion form factor fitting.]] |
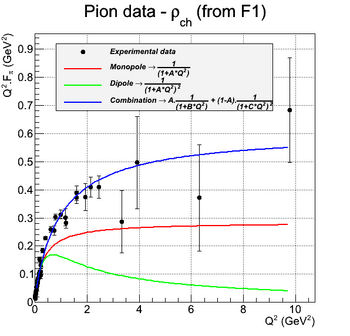
| − | | | + | | style="width: 50%;" | [[File:Pion_FF_Fitting_q2f.png|thumb|center|350px|Pion form factor fitting.]] |
| + | |} | ||
| + | |||
| + | |||
| + | {| border="0" style="text-align:center;" width="70%" | ||
| + | |- | ||
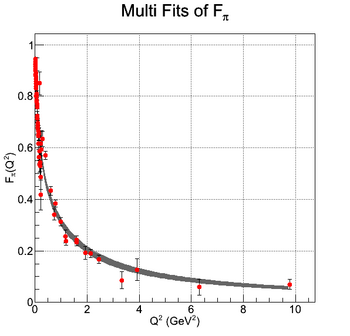
| + | | style="width: 50%;" | [[File:Pion_FF_MultiFit.png|thumb|center|350px|Multi fit of the pion form factor.]] | ||
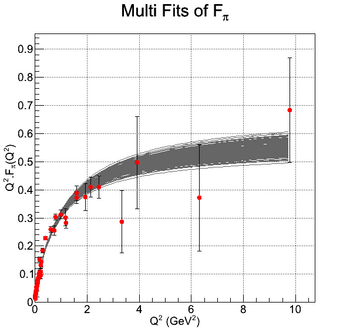
| + | | style="width: 50%;" | [[File:Pion_FF_MultiFitQ2.png|thumb|center|350px|Multi fit of the pion form factor.]] | ||
| + | |} | ||
| + | |||
| + | {| border="0" style="text-align:center;" width="100%" | ||
| + | |- | ||
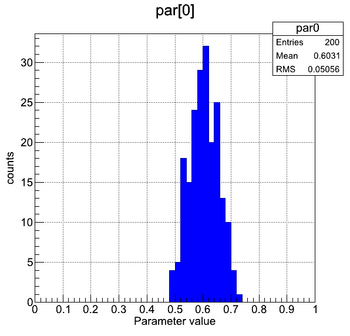
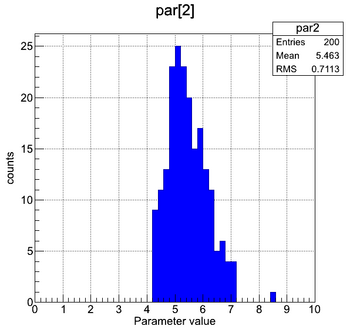
| + | | style="width: 33%;" | [[File:Pion_FF_MultiFit_par0.png|thumb|center|350px|Multi fit - distribution of fitted parameter #0.]] | ||
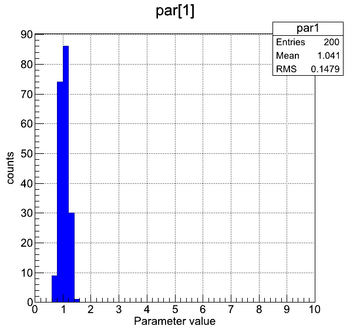
| + | | style="width: 34%;" | [[File:Pion_FF_MultiFit_par1.png|thumb|center|350px|Multi fit - distribution of fitted parameter #1.]] | ||
| + | | style="width: 33%;" | [[File:Pion_FF_MultiFit_par2.png|thumb|center|350px|Multi fit - distribution of fitted parameter #2.]] | ||
|} | |} | ||
Latest revision as of 14:16, 27 August 2012
| ⇐ Back to the Main_Page |
Transverse Charge Distribution of Hadrons
This work is done by the Nuclear Physics Group at the CUA, together with Dr. Gerald A. Miller, from the University of Washington.
According to Siddharth Venkat, 2010, having the form factor F(Q^2) of a particle it is possible to simplify the calculation of its two-dimensional transverse density using the finite radius approximation.
In this work we are going to calculate the transverse charge distribution of Pions. As a first step for this calculation, we are reproducing the Proton charge distribution from Siddharth Venkat, 2010.
The equation: <math> \frac{1}{2} </math>
Charged Pion Transverse Charge Distribution
Proton Transverse Charge Distribution
This section is a reproduction of the calculation done in [Siddharth Venkat, 2010], using experimental data from ... (insert references here!)
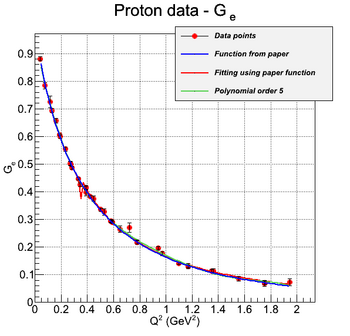
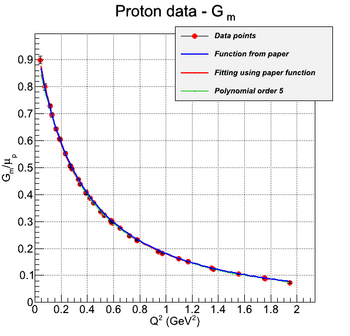
In the case of protons, the measured form factors are G_e and G_m. They are linear combinations of F1 and F2, according to the following equations:
(insert equations)
The experimental data and the fit given by [Siddharth Venkat, 2010] for G_e and G_m are shown in the following figures:
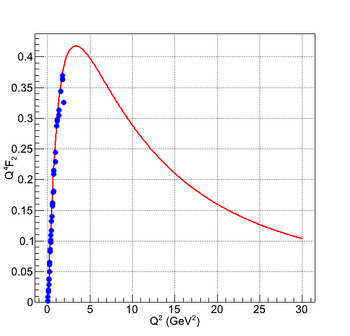
These G_e and G_m form factors can be re-written in the F_1 and F_2 form factors. The results are shown in the following figures:
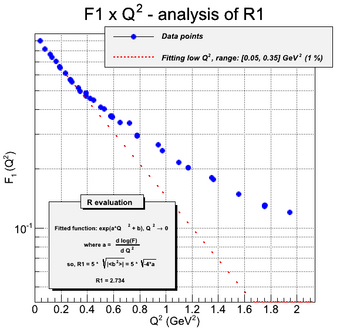
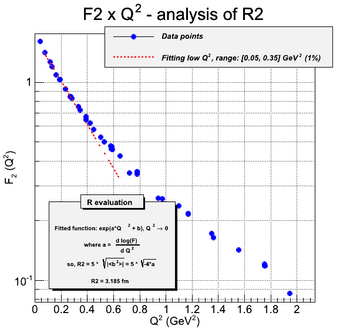
As the charge distribution are Fourier transforms of form factors, one can extract the charge distribution by performing this calculation. The first step is to calculate the mean radius of the proton. It is done by fitting the form factors in the limit of low Q^2.
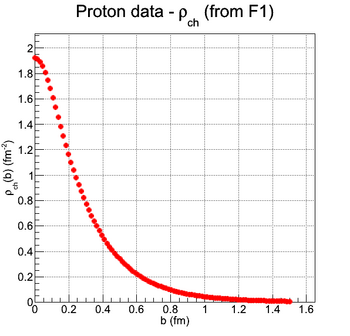
Finally, the charge distribution can be calculated by a truncated expansion in Bessel Functions. The truncation is required by the limitation in knowledge of the form factor with Q^2. The following figure shows the calculated charge distribution from the fitted function of G_e and G_m given in [Siddharth Venkat, 2010] and also R_1 and R_2 of this paper.
The next step of this calculation is the estimation of uncertainties. There are two main sources of uncertainties:
- Form factor uncertainties, from experimental data
- Incompleteness error, from the truncation of the expansion (limitation of the knowledge of form factors for high Q^2).