Pion and Kaon Structure Functions

⇐ Back to the Main_Page

Parton Distributions in Pion and Kaon

The structure functions in terms of sea quarks and gluons are expected to be different for pions, kaons, and nucleons and to provide basic information about their origin of mass.

Experimental data are sparse. As a result, there has been persistent doubt about the behavior of the pion's valence quark structure function at large Bjorken-x and virtually nothing is known about the contribution of sea quarks and gluons. The Electron-Ion Collider with an acceptance optimized for forward physics has the potential for accessing pion and kaon structure functions over a large kinematic region through the Sullivan process. This would allow for measurements testing if the origin of mass is encoded in the differences of gluons in pions, kaons, and nucleons, and measurements that could serve as a test of assumptions used in the extraction of structure functions and the pion and kaon form factors.

In this work we are going to calculate structure functions for pion and kaon from the Sullivan process with flexible choices of x and Q2 bins, and evaluate the uncertainties and potential to constrain, e.g. the gluon PDFs.

References

• J.F. Owens, Phys. Rev. D, Vol. 30, Issue 5 (1984), 943.

• M. Glueck, E. Reya, A. Vogt, Z. Phys. C 53 (1992), 651.

• M. Alberg, E. M. Henley, Phys. Lett. B611 (2005) 111.

• M. Alberg, J. Tibbals, Phys. Lett. B709 (2012) 370.

Proton Transverse Charge Distribution

This section is a reproduction of the calculation done in [Siddharth Venkat, 2010], using experimental data from ... (insert references here!)

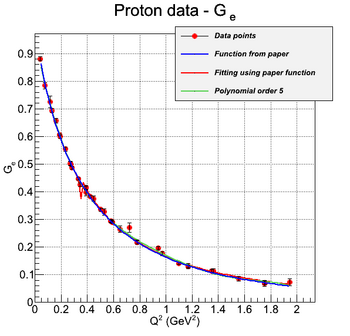
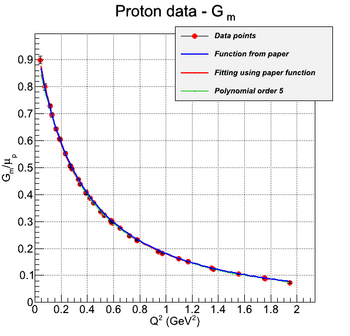
In the case of protons, the measured form factors are G_e and G_m. They are linear combinations of F1 and F2, according to the following equations:

(insert equations)

The experimental data and the fit given by [Siddharth Venkat, 2010] for G_e and G_m are shown in the following figures:

Proton form factor G_e. Experimental data from XX and fit from [Siddharth Venkat, 2010].

Proton form factor G_m. Experimental data from XX and fit from [Siddharth Venkat, 2010].

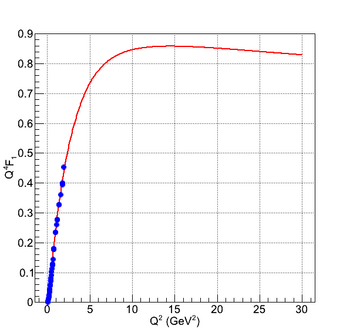
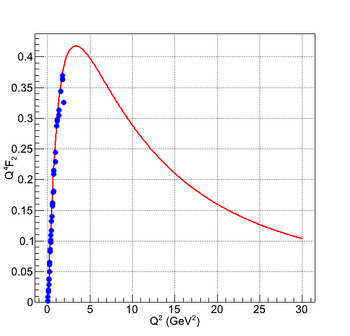
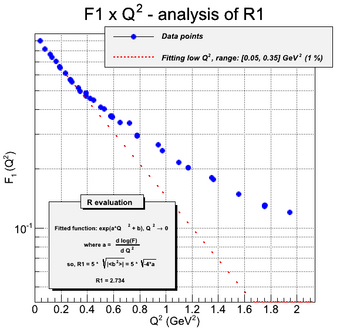
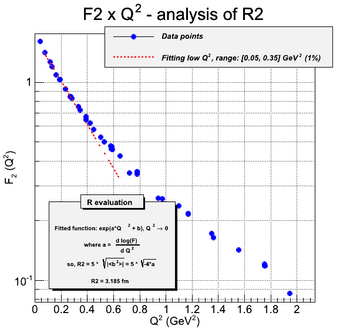
These G_e and G_m form factors can be re-written in the F_1 and F_2 form factors. The results are shown in the following figures:

Proton form factor F_1(Q^2).

Proton form factor F_2(Q^2).

As the charge distribution are Fourier transforms of form factors, one can extract the charge distribution by performing this calculation. The first step is to calculate the mean radius of the proton. It is done by fitting the form factors in the limit of low Q^2.

Mean radius R_1 of the proton, related to the form factor F_1. Value fitted in the paper was 3.29 fm.

Mean radius R_2 of the proton, related to the form factor F_2. Value fitted in the paper was 3.62 fm.

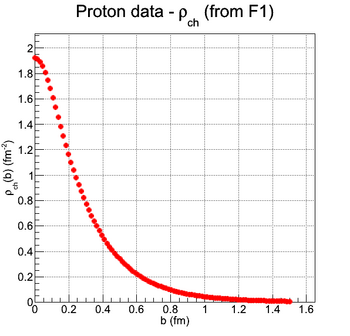
Finally, the charge distribution can be calculated by a truncated expansion in Bessel Functions. The truncation is required by the limitation in knowledge of the form factor with Q^2. The following figure shows the calculated charge distribution from the fitted function of G_e and G_m given in [Siddharth Venkat, 2010] and also R_1 and R_2 of this paper.

Calculated transverse proton distribution from .

The next step of this calculation is the estimation of uncertainties. There are two main sources of uncertainties:

• Form factor uncertainties, from experimental data
• Incompleteness error, from the truncation of the expansion (limitation of the knowledge of form factors for high Q^2).