MainPage:Nuclear:ChargeDistribution

⇐ Back to the Main_Page

Transverse Charge Distribution of Hadrons

This work is done by the Nuclear Physics Group at the CUA, together with Dr. Gerald A. Miller, from the University of Washington.

According to Siddharth Venkat, 2010, having the form factor F(Q^2) of a particle it is possible to simplify the calculation of its two-dimensional transverse density using the finite radius approximation.

In this work we are going to calculate the transverse charge distribution of Pions. As a first step for this calculation, we are reproducing the Proton charge distribution from Siddharth Venkat, 2010.

The equation: <math> \frac{1}{2} </math>

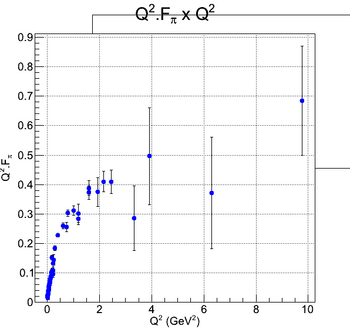
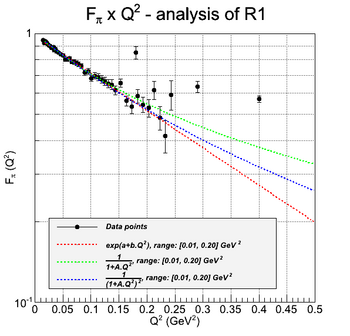
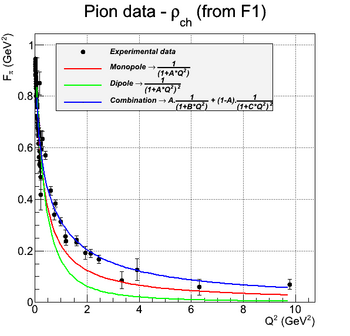
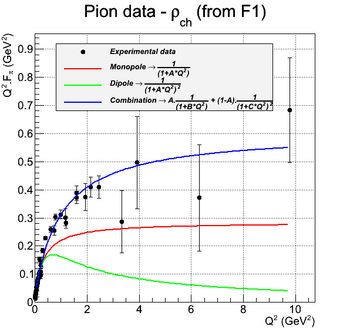
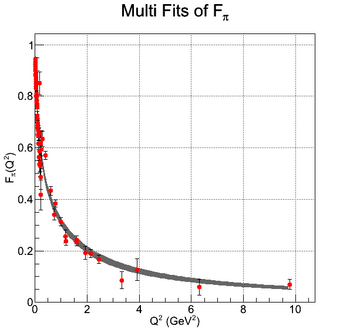
Charged Pion Transverse Charge Distribution

Pion form factor.

Fitting of the pion form factor for low Q^2, for finding its mean radius.

Pion form factor fitting.

Pion form factor fitting.

Multi fit of the pion form factor.

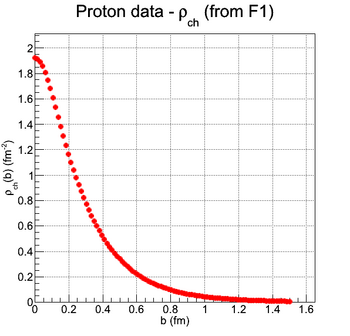
Proton Transverse Charge Distribution

This section is a reproduction of the calculation done in [Siddharth Venkat, 2010], using experimental data from ... (insert references here!)

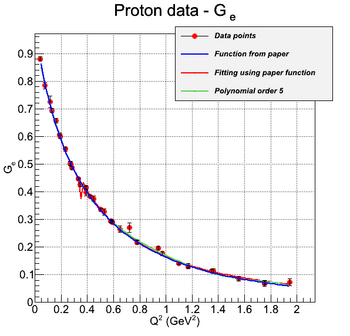
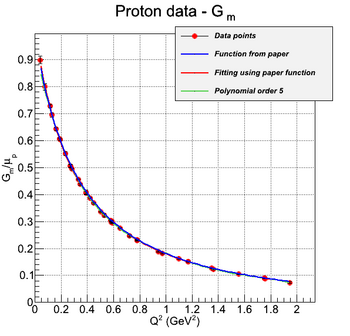
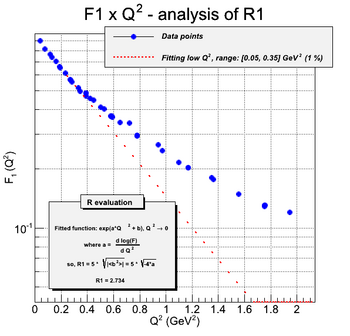
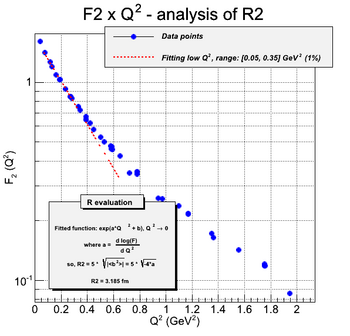
In the case of protons, the measured form factors are G_e and G_m. They are linear combinations of F1 and F2, according to the following equations:

(insert equations)

The experimental data and the fit given by [Siddharth Venkat, 2010] for G_e and G_m are shown in the following figures:

Proton form factor G_e. Experimental data from XX and fit from [Siddharth Venkat, 2010].

Proton form factor G_m. Experimental data from XX and fit from [Siddharth Venkat, 2010].

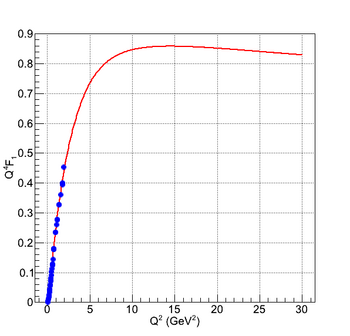
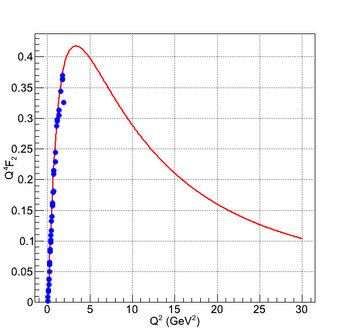
These G_e and G_m form factors can be re-written in the F_1 and F_2 form factors. The results are shown in the following figures:

Proton form factor F_1(Q^2).

Proton form factor F_2(Q^2).

As the charge distribution are Fourier transforms of form factors, one can extract the charge distribution by performing this calculation. The first step is to calculate the mean radius of the proton. It is done by fitting the form factors in the limit of low Q^2.

Mean radius R_1 of the proton, related to the form factor F_1. Value fitted in the paper was 3.29 fm.

Mean radius R_2 of the proton, related to the form factor F_2. Value fitted in the paper was 3.62 fm.

Finally, the charge distribution can be calculated by a truncated expansion in Bessel Functions. The truncation is required by the limitation in knowledge of the form factor with Q^2. The following figure shows the calculated charge distribution from the fitted function of G_e and G_m given in [Siddharth Venkat, 2010] and also R_1 and R_2 of this paper.

Calculated transverse proton distribution from .

The next step of this calculation is the estimation of uncertainties. There are two main sources of uncertainties:

• Form factor uncertainties, from experimental data
• Incompleteness error, from the truncation of the expansion (limitation of the knowledge of form factors for high Q^2).