MainPage:Nuclear:Summer2019:PWO

From cua_phy
Jump to navigation Jump to search

Lead Tungstate Crystal 3D Mapping

Summary

Since crystals are grown, there are imperfections in the quality of crystals. To check the quality of each crystal, transverse optical transmittance measurements are taken. To represent the resulting data, a 3D map was developed through CERN’s ROOT. This application allows the user to easily identify sub-standard crystals and locate imperfections within the crystal.

Introduction

Lead tungstate (PWO) crystals act as scintillators in electromagnetic calorimeters. This type of calorimeter measures the energy of particles that interact via the electromagnetic force (Bock).

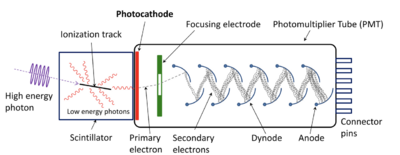
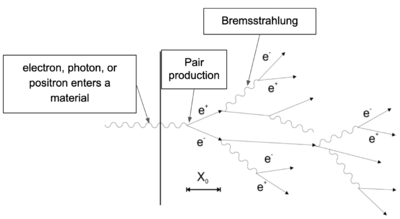
Figure 1 - Scintillator Counter Diagram.


Figure 2 - Electromagnetic Shower Diagram.

As seen in Figure 1, when a high-energy photon, electron, or positron enters the PWO crystal, it scintillates and produces photons. Figure 2 breaks down the process of scintillation and how a electromagnetic showers occurs. The high-energy incoming particle causes pair production which results in an electron and positron. As the electron and positron travels through the particle, Bremsstrahlung (energy losses as a charged particle accelerates around a nucleus) occurs and photons are emitted. These photons can cause another cycle of pair production and Bremsstrahlung until all the energy has been deposited into the crystal (Landau and Rummer).

Next, in figure 1, the photomultiplier tube converts incident photons into a signal. Specifically, these photons interact with a photocathode which produces electrons through the photoelectric effect. However, this signal is too weak to detect, so it must be amplified. The primary electron is directed by a magnetic field towards a dynode. When the primary electron interacts with the dynode, it creates multiple secondary electrons which travel to another dynode for further amplification. Eventually, a signal can be detected and the operator can measure the energy of the incoming particle (Glenn).

Additionally, lead tungstate is ideal as a scintillator in a compact electromagnetic calorimeter due to the following properties: high density (8.3 g/cm3), short radiation length (0.89 cm), small Moliere radius (2.2 cm), and fast scintillation time (80% in 25ns) (CMS Physics Technical Design Report). Despite this, the manufacturing process of crystals are yet to be perfected. As seen in the following sections, there can be significant variations in the transverse optical transmittance of these crystals. Thus, it’s important to select high-quality crystals. Developing a 3D map would allow easier identification of imperfections in the crystal because the user could visually identify and locate the imperfections.

Method

Crystal Preparation

Each lead tungstate crystal was thorougly cleaned with 70% isopropyl alcohol and dried with a Kimwipes. Also, temporarily remove the label as it interferes with the measurement. Although the crystal are dense, they are very brittle and easy to chip. Be sure to handle with care and use gloves at all times.

Lambda 950 Spectrophotometer

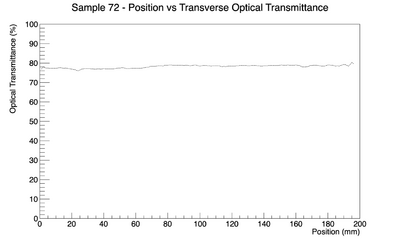
The transverse optical transmittance of each crystal was measured using the Lambda 950 Spectrophotometer. An apparatus with a stepper motor was installed to slide the crytal along its longitudinal axis. The stepper motor moved 1 mm per second. At the start of calibration and every trial, the whole apparatus was covered in a black cloth to prevent any light from entering into the chamber. The optical transmittance was auto-zeroed after changing each wavelength and the iris was set to 2.0 mm. Usually, the the wavelength 360 nm was used as it created higher amounts of deviance to allow easier identification of imperfections.

Crystal Orientation

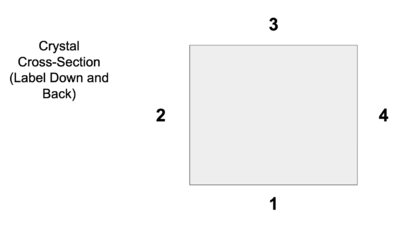
Figure 3 - Crystal Orientation diagram.

Place the end of the crystal with the (now removed) label in the back. As seen in the diagram, side 1 is with the label down.

Data Processing

Open the *.csv files with Microsoft Excel. For a plot or 2D map, delete the column with time and cut the optical transmittance measurements. Usually, the cut optical transmittance measurement should vary by 2% on the ends. Then, save the spreadsheet as a tab-delimited text file. To input the data into the application, don't forget to change the name of the file it reads in.

Application Development

ROOT

Developed by CERN, ROOT is an object-oriented program and library that is designed to efficiently handle large amounts of data. As of August 2019, it is written in C++.

Recommended Resources for Beginners (as of ROOT 6.18.0 )

Simple Plot

Figure 4 - Example of a crystal plot with ROOT.
{
    g = new TGraph("Sample72_1.txt"); // Reads data from a .txt file. CHANGE AS NEEDED
    g->SetMinimum(0);
    g->SetMaximum(100);
    g->GetXaxis()->SetLimits(0, 200);
    g->SetTitle("Sample 72 - Position vs Transverse Optical Transmittance; Position (mm); Optical Transmittance (%)");
    g->SetMarkerStyle(7);
    g->Draw("ALP");
}

The .txt files have one column of transverse optical transmittance data and are stored in the tab-delimited text file format. This .txt file was made from Microsoft Excel and cut at the edges.

Simple Plot - Sample Files

2D Map

Figure 5 - Example of a 2D Map with ROOT. This map only shows one face using a similar .txt file from before.
TCanvas *th2polyBoxes()

#include <fstream>
#include <iostream>
#include <stdio.h>
#include <fstream>


void Crystal72_2D_2(){

  struct input_t
    
  //Define array  structure for input
    
  {       
    Double_t transmittance;
  };
 
  input_t input;
 
  // Reads data from ONE column of data
 
  FILE *f = fopen("Crystal5478_620.txt","r"); // Reads data from a .txt file. CHANGE AS NEEDED 
  char line[400];
 
  // Creates array

  Double_t transArray[196];

 
  Int_t j=0;
  TFile *file = new TFile("test.root","RECREATE");
  for(Int_t i;fgets(&line[0],500,f);i++){  
    if (line[0] == '#'){
      continue;
    }else{
      sscanf(&line[0], "%lf", &input.transmittance);
    }

      transArray[j]=input.transmittance;
      j++;
      
   }

 
  //Finds the average
  float avg = 0.0;
  float sum = 0.0;
  int size;
 
  size = sizeof(transArray) / sizeof(transArray[j]);

  for (int i = 0; i < size; ++i)
   {
   sum += transArray[i];
  }
  avg = ((float)sum)/size; //or cast sum to double before division

  cout << "Average  " << avg << "\n";

  // Calcuates deviance
 
  Double_t dev[size];
 
  for(int i = 0; i < size-1; i ++)
  {
      dev[i]= transArray[i] - avg;
      //cout << "Deviance  " << dev[i] << "\n";
  }


  //Set-up canvas/graph

  TCanvas *ch2p2 = new TCanvas("ch2p2","ch2p2",1435,415);
  gStyle->SetPalette(kRainBow);
  TH2Poly *h2p = new TH2Poly();
  h2p->SetName("Boxes");
  h2p->SetTitle("Boxes");
  Int_t i,l;
  Int_t nx = size;
  Int_t ny = 1;
  Double_t xval1,yval1,xval2,yval2;
  Double_t dx=1, dy=4;
  xval1 = .5;
  xval2 = dx + xval1;
  yval1 = -4;
  yval2 = dy;

  // In the x, there is a bin per mm.
  // In the y, there is only one bin. In this sense, "y" is meaningless.
  // Optical transmittance is reflected in the z.


  // This "for" loop adds "nx" bins in increments of "dx".
  for (i = 0; i<nx; i++) {
     h2p->AddBin(xval1, yval1, xval2, yval2);
     xval1 = xval2;
     xval2 = xval2+(dx);
     
     //Since y is meaningless, the weight is used to create the different shades of color
     
     h2p->Fill(i, .1 , dev[i]);
  }

  // Sets the range and removes the y-axis.
 
  h2p->GetXaxis()->SetRangeUser(0,200);
  h2p->GetYaxis()->SetRangeUser(0,100);
  h2p->GetZaxis()->SetRangeUser(-3,3);
  h2p->GetYaxis()->SetLabelOffset(999);
  h2p->GetYaxis()->SetLabelSize(0);
 

  // Sets the title, removes the stats box, and draws graph.
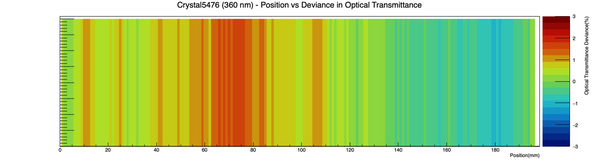
  h2p->SetTitle("Crystal5476 (360 nm) - Position vs Deviance in Optical Transmittance; Position(mm); ;Optical Transmittance Deviance(%)");
  h2p->GetZaxis()->SetTitleOffset(0.5);
  h2p->SetStats(0);
  h2p->Draw("COLZ");
   
  return ch2p2;
}

2D Map - Sample files

3D Map

Figure 6 - Example of a 3D map with ROOT. Note: This is only a snapshot. The application allows tilt and zoom.
namespace {

Double_t my_transfer_function(const Double_t *x, const Double_t * /*param*/)
{

  if (*x>-.0001 && *x<.0001)
      return 0.001;
   return 1.;
}
}

void glgraph(){

int data = 0;

// Reads data in
   
ifstream file { "5608.txt" }; // Reads data from a .txt file. CHANGE AS NEEDED 
if (!file.is_open()) return -1;

double transArray [200][4]{};
 
for (int i{}; i != 200; ++i) {
    for (int j{}; j != 4; ++j) {
        file >> transArray[i][j];
        
    }
}


  // Calculates the average
  float avg = 0.0; 
  float sum = 0.0;
  int size;

  for (int i{}; i != 200; ++i) {
    for (int j{}; j != 4; ++j) {
    size = sizeof(transArray) / sizeof(transArray[i][j]     
 );
  sum += transArray[i][j];
    }
  }
  avg = ((float)sum)/size;

  double dev[size][4];

  cout << "Average Optical Transmittance  " << avg << "\n";

  char average[64];
  int ret = snprintf(average, sizeof average, "%f", avg);

if (ret < 0) {
    return EXIT_FAILURE;
}
if (ret >= sizeof average) {
    //Result was truncated - resize the buffer and retry.
}

// Calculate deviance and stores it into an array
  
 for (int i{}; i != 195; ++i) {
    for (int j{}; j != 4; ++j) {
      dev[i][j]= transArray[i][j] - avg;
    }}

// Sets the parameters for the 3D map
 
 TH3F *hist = new TH3F("glvoxel", "OT", (size/4), 0., (size/4), 20, 0., 20., 20, 0., 20.);

   for (UInt_t i = 0; i < 200; ++i) {
     for (Int_t j = 1; j< 19;j++){
       hist->Fill(i, j, 0., dev[i][0]); //Side 1
       hist->Fill(i, 19.9, j, dev[i][1]); //Side 2
       hist->Fill(i, j, 19.9, dev[i][2]); // Side 3
       hist->Fill(i, 0.1,j , dev[i][3]); // Side 4
       }
    }
     
   
   gStyle->SetCanvasPreferGL(1);
   hist->Draw("glcolz");

// Label and set ranges for x-axis, y-axis, and z-axis
   hist->GetXaxis()->SetTitle("Length (mm)");
   hist->GetXaxis()->SetTitleOffset(1.5);
   hist->GetYaxis()->SetTitle("Width (mm)");
   hist->GetYaxis()->SetTitleOffset(1.5);
   hist->GetZaxis()->SetTitle("Height (mm)");
   hist->GetZaxis()->SetTitleOffset(1.5);
   hist->GetZaxis()->SetRangeUser(-10,0);
   
   hist->SetTitle("OT");
   gStyle->SetCanvasPreferGL(1);
   gStyle->SetPalette(kRainBow);
   hist->SetFillColor(9);
   hist->Draw("glcolz");

// Creates the title for the 3D map
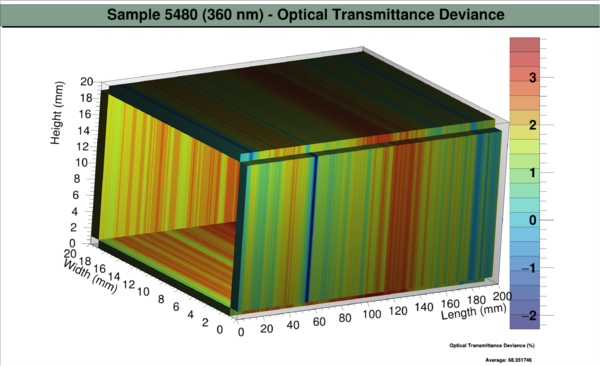
   TPaveLabel *title = new TPaveLabel(-1., 0.86, 1., 0.98, "Sample 5608 (Bubbles) (360 nm) - Optical Transmittance Deviance");
   
   TLatex *tex = new TLatex(0.75,0.05,"Optical Transmittance Deviance (%)");
  tex->SetNDC();
  tex->SetTextSize(.015);
  tex->SetLineWidth(2);
  tex->Draw();
  title->SetFillColor(32);
  title->Draw();
 

// Outputs the average  
  TLatex *avg3 = new TLatex(0.81, 0.01, TString::Format("Average: %s", average));
  avg3->SetNDC();
  avg3->SetTextSize(.015);
  avg3->SetLineWidth(2);
  avg3->Draw();
  title->SetFillColor(32);
  title->Draw();

   //Now, specify the transfer function.
   TList * lf = hist->GetListOfFunctions();
   if (lf) {
      TF1 * tf = new TF1("TransferFunction", my_transfer_function);
      lf->Add(tf);
   }
}

The .txt files is similar to the ones from the 2D map except it has 4 columns. Each position is linked to the column number according to the following figure. Position 1 is with the label down.

3D Map - Sample files

Data Analysis

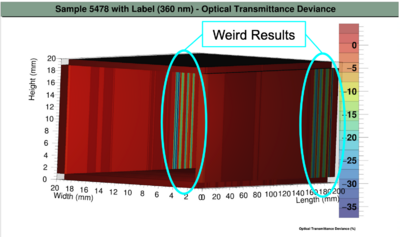
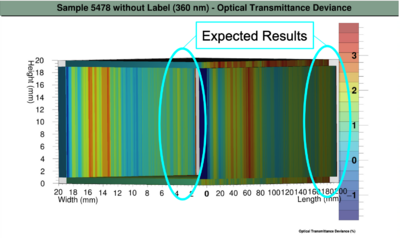
Crystal 5478 (Label Interference)

Figure 7 - First 3D map. Crystal has a label.

With the first measurement, there were weird dips on the rear sides (position 2 & 4) of the crystal. Since the label is towards the rear, the interference is probably from the label. The label usually does not interfere with the map since its always facing down. However, since positions 2 & 4 place the label on the side, it interferes with the measurement.

Figure 8 - Second 3D map. Crystal does not a label.

With the label removed, the measurements are what was expected. This occurrence supports the idea that labels interfere with the measurements. Thus, the label was removed for every crystal thereafter.

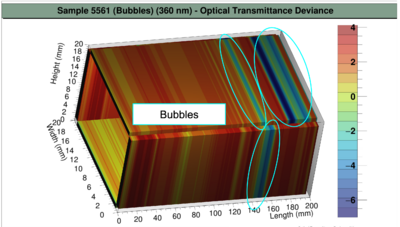
Crystal 5561 (Bubbles)

Figure 9 - Enhanced picture of Crystal 5561

Crystal 5561 was identified to have bubble-like imperfections after shining a laser through it. So, the 3D map was tested to see if it could identify the imperfections in the crystal.


Figure 10 - 3D map of Crystal 5561

The places with the dips in optical transmittance are similar in position to the one in the photo. So, this supports that the 3D map could allow easy identification of bubble-like imperfections.

Crystal 5609 (Chipped)

Figure 11 - 3D map of Crystal 5561

After an incident, crystal 5609 had a 2 cm chip on side 3.


Figure 12 - 3D map of Crystal 5561

The chip can easily be seen on both sides of the crystal as marked by the blue bands. However, in the 3D map, it is only 2 cm on one side and 1 cm on the other side. Thus, this irregularity suggests that the beam is not perfectly centered. Instead, it measures the optical transmittance below the center. In further measurements, it would be interesting to take more off-axis measurements to build a higher resolution map.

Crystal 5480 (Fingerprint)

Figure 13 - 3D map of Crystal 5561 with fingerprint.

As seen in the above figure, the fingerprint are easily seen by the blue bands.

Conclusion

Unlike longitudinal measurements which only record one area, the transverse transmittance measures along the length of the crystal. Thus, with the 3D map, one could more accurately identify and locate imperfections such as bubbles and chips in the crystal. Furthermore, the interference of items such as fingerprints and labels underlined the importance of thoroughly cleaning the crystal. However, the 3D map system is limited in the transverse transmittance measurements only takes data on axis. As an extension, one could develop a system to measure off-axis, which would increase the resolution of the 3D map to pick-up smaller imperfections.

Presentations

Week 2

Week 3

Week 4

Other Projects

KaonLT - Stacking Histograms

Overview: The KaonLT experiment takes measurements of the L/T separated kaon electroproduction cross section. These measurement are important to ehance our understanding of the kaon's structure.

Figure 14 - Example of stacking two histograms with ROOT.

Purpose: After receiving data, cuts are made. To compare the cuts, an application needs to be developed to graph the pre-cut and post-cut data on the same histogram. Additionally, since data is stored in a tree, the program must identify the correct user-selected leaf from each root file.

In the attached sample file, the user only applied cuts to the TDCTimeRaw plots. Applying cuts to the TDCTimeRaw plots affects the TDCTime plots. TDCTime plots only shows accepatable physics coincidence events, so TDCTimeRaw and TDCTime plots should differ slightly. 

//Modified script from Richard Trotta.
#include <string>
#include <cstdio>
#include <iostream>


void plot_Stat2(Int_t runNum = 4889, Int_t numEvts = 0, TString leaf = ""){

   if(runNum==0){
  
  	cout << "Please enter run number ...\n";
  	cin >> runNum;
	}
  
   /* if(numEvts==0){
  
  	cout << "Please enter number of events in replay ...\n";
  	cin >> numEvts;
	}*/

   if(leaf==""){
  
  	cout << "Please pick a leaf ...\n";
  	cin >> leaf;
	}

    TString rootfile1 = Form("/Applications/root_v6.18.00/macros/Overlap/coin_replay_production_%i_cut", runNum);

  TString outputhist1;
  outputhist1 = rootfile1 + ".root";
  
  TString outputpdf1;
  outputpdf1 =  Form("OUTPUT/statsPlots_%i.pdf",runNum);
  
  TFile *f1 = TFile::Open(outputhist1);
  if( !f1 || f1->IsZombie()){
	return;
  }
 
  TString rootfile2 = Form("/Applications/root_v6.18.00/macros/Overlap/coin_replay_production_%i_nocut", runNum);

  TString outputhist2;
  outputhist2 = rootfile2 + ".root";
  
  TString outputpdf2;
  outputpdf2 =  Form("OUTPUT/statsPlots_%i.pdf",runNum);
  
  TFile *f2 = TFile::Open(outputhist2);
  if( !f2 || f2->IsZombie()){
	return;
  }
  
  TString cutLeaf, nocutLeaf, deltaLeaf,xptarLeaf, yptarLeaf, wLeaf;
  
  TTreeReader r("T", f1);
  TTreeReader n("T", f2);

  TCanvas *c1 = new TCanvas("c1","Stat plots", 600, 400); 
  // TCanvas *c2 = new TCanvas("c2","Stat plots", 600, 400);
  //TCanvas *c3 = new TCanvas("c3","Stat plots", 600, 400);
  //TCanvas *c4 = new TCanvas("c4","Stat plots", 600, 400);

  TH1F *h1 = new TH1F("h1", Form("Run %i ; T.coin.pDCREF1_tdcTimeRaw", runNum), 500,15200,16600);
  // TH1F *h1 = new TH1F("h1", Form("Run %i - Uncut(Blue) vs Cut(Red); %s", runNum, leaf), 300,200,500);
  //TH2F *h2= new TH2F("h2","Xptar vs Yptar", 200, -0.1, 0.1,200,-0.1, 0.1);
  //TH2F *h3= new TH2F("h3","W^2 vs Xptar ", 200, -.1, .1,200,0, 20);
  //TH2F *h4= new TH2F("h4","W^2 vs Yptar ", 200, -.1, .1,200,0, 20);

  TH1F *h2 = new TH1F("h2","Uncut", 500,15200,17000);
  
  //if(spec == "hms"){
  cutLeaf = leaf;
  nocutLeaf = leaf;
  /* xptarLeaf = "H.gtr.th";
    yptarLeaf = "H.gtr.ph";
    //deltaLeaf = "H.gtr.dp";
    wLeaf = "H.kin.W2";*/
     TTreeReaderValue<Double_t> cut(r, cutLeaf);
     TTreeReaderValue<Double_t> nocut(n, nocutLeaf);
     /* TTreeReaderValue<Double_t> yfp(r, yfpLeaf);
  TTreeReaderValue<Double_t> xptar(r, xptarLeaf);
  TTreeReaderValue<Double_t> yptar(r, yptarLeaf);
  TTreeReaderValue<Double_t> invmass(r, wLeaf);*/
     //TTreeReaderValue<Double_t> hsdelta(r,deltaLeaf);
   while(r.Next()){
      
     /*int k;
     cout << "While loop W^2 " << k << '\n';
      if(*hsdelta > -8 && *hsdelta < 8
	){*/
	
     h1->Fill(*cut);
	//h2->Fill(*yptar,*xptar);
	//h3->Fill(*xptar,*invmass);
	//h4->Fill(*yptar,*invmass);
	
	/*	k++;
		}*/
      
       }

   h1->Draw();
   h1->SetLineColor(kMagenta);
   h1->SetLineWidth(2);
  
  while(n.Next()){
      
    /*int k;
     cout << "While loop W^2 " << k << '\n';
      if(*hsdelta > -8 && *hsdelta < 8
	){*/
	
	h2->Fill(*nocut);
	//h2->Fill(*yptar,*xptar);
	//h3->Fill(*xptar,*invmass);
	//h4->Fill(*yptar,*invmass);
	
	/*	k++;
		}*/
      
       } 
   //h1->GetXaxis()->SetTitle("yfp");
   //h1->GetYaxis()->SetTitle("");

  //h2->GetXaxis()->SetTitle("yptar");
    //h2->GetYaxis()->SetTitle("xptar");

  //h3->GetYaxis()->SetTitle("W^2");
  //h3->GetXaxis()->SetTitle("xptar");

  //h4->GetYaxis()->SetTitle("W^2");
  //h4->GetXaxis()->SetTitle("yptar");

  //c1->Divide(2,2);
  //c1->cd(1);
  gStyle->SetOptStat(0);
  h2->SetLineColor(kBlue+4);
  h2->SetLineWidth(2);
  h2->Draw("SAME");
  //h1->SetStats(1111)

   auto legend = new TLegend(0.8,0.8,0.9,0.9);
   legend->SetHeader("Legend","C"); // option "C" allows to center the header
   legend->AddEntry("h1","Cuts","l");
   legend->AddEntry("h2","No cuts","l");
   legend->Draw();
   
  //c1->Print(outputpdf1+"(");
  //c1->cd(2);
  //h2->Draw("Colz");
  //c2->Print(outputpdf+ ")");
  //c1->cd(3);
  //h3->Draw("Colz");
  //c3->Print(outputpdf);
  //c1->cd(4);
  //h4->Draw("Colz");
  //c4->Print(outputpdf+")");

  //c1->Print("OUTPUT/pngFiles" + spec + "_statsPlots_" + Form("%i",(int)runNum) + ".png");

  /*const string sep = " |";
  const int total_width = 154;
  const string line = sep+ string(total_width-1,'-') + '|';

  ofstream myfile;*/
   

  /*if(spec=="shms"){
    xfpLeaf = "P.dc.x_fp";
    yfpLeaf = "P.dc.y_fp";
    xptarLeaf = "P.gtr.th";
    yptarLeaf = "P.gtr.ph";
    deltaLeaf = "P.gtr.dp";
  TTreeReaderValue<Double_t> xfp(r, xfpLeaf);
  TTreeReaderValue<Double_t> yfp(r, yfpLeaf);
  TTreeReaderValue<Double_t> xptar(r, xptarLeaf);
  TTreeReaderValue<Double_t> yptar(r, yptarLeaf);
  TTreeReaderValue<Double_t> invmass(r, wLeaf);
  TTreeReaderValue<Double_t> ssdelta(r,deltaLeaf);
    while(r.Next()){
      
      int k;
      cout << "While loop W^2 " << k << '\n';
      
      if(*ssdelta > -10 && *ssdelta < 15
	 ){
	
	h1->Fill(*yfp,*xfp);
	//h2->Fill(*yptar,*xptar);
	
	k++;
      }
      
      }*/
  
  //h1->GetXaxis()->SetTitle("yfp");
  //h1->GetYaxis()->SetTitle("xfp");

  //h2->GetXaxis()->SetTitle("yptar");
  //h2->GetYaxis()->SetTitle("xptar");

  //h3->GetYaxis()->SetTitle("W^2");
  //h3->GetXaxis()->SetTitle("xptar");

  //h4->GetYaxis()->SetTitle("W^2");
  //h4->GetXaxis()->SetTitle("yptar");

  //c1->Divide(2,2);
  //c1->cd(1);  
  //c1->Print(outputpdf+"");
  //c1->cd(2);
  //h2->Draw("Colz");
  //c2->Print(outputpdf+ ")");
  //c1->cd(3);
  //h3->Draw("Colz");
  //c3->Print(outputpdf);
  //c1->cd(4);
  //h4->Draw("Colz");
  //c4->Print(outputpdf+")");

  c1->Print(Form("/Applications/root_v6.18.00/macros/Overlap/Output/statsPlots_%i_.pdf",(int)runNum));

  /*const string sep = " |";
  const int total_width = 154;
  const string line = sep+ string(total_width-1,'-') + '|';

  ofstream myfile;
  }*/



}

Sample Files - Stacking Histograms

Works Cited

Bock, Rudolf K. “Calorimeter.” Calorimeter , CERN, 9 Sept. 1998, <http://web.archive.org/web/20071220021724/http://rd11.web.cern.ch/RD11/rkb/PH14pp/node19.html>.

CMS Physics Technical Design Report. CERN, 2006, CMS Physics Technical Design Report.

Glenn F Knoll. Radiation Detection and Measurement, Third Edition 2000. John Wiley and Sons , ISBN 0-471-07338-5

Landau, Lev Davydovitch, and G. Rumer. “The Cascade Theory of Electronic Showers.” The Royal Society of Mathematical, Physical, and Engineering Sciences , 18 Nov. 1937.

Retrieved from "https://www.vsl.cua.edu/cua_phy/index.php?title=MainPage:Nuclear:Summer2019:PWO&oldid=9340"