MainPage:Nuclear:Summer2013:AerogelCharacterization
| ⇐ Back to Summer 2013 |
| ⇐ Back to the Main_Page |
Project Overview
At the Jefferson Lab, aerogel is used in one of the particle detectors to distinguish kaons and protons that detach from the nucleus of an atom when it is hit with an electron. The kaon or proton travels through the aerogel faster than light can travel through the aerogel causing Cerenkov radiation. Kaons have a different threshold than the proton and therefore they can be identified when traveling through the aerogel at a certain momentum.
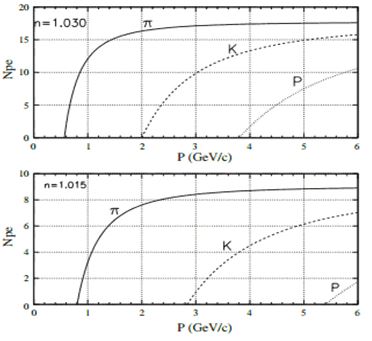
Depending on the refractive index the difference between the kaons an protons or pions and kaons is more identifiable, see chart below. The refractive index is directly related to the density of the aerogel. In order to maintain the density, and therefore the refractive index, of the aerogel it is important to make sure that the aerogel does not absorb any water. The most likely source of water is the humidity in the air. Therefore the affect of humidity on aerogel is being tested. Aerogel from two different companies, the Matsushita Lectric Works, Ltd and the Japan Fine Ceramic, are being tested.
Brief description of goals
1. Identify the refractive index (n) experimentally in order to know what particles can best be detected when shot through it.
2. Test the affect of humidity on aerogel by putting it in an area of controlled humidity and then retesting for the refractive index.
Refractive Index
Using Snell's Law on the two faces of the aerogel where the light changes mediums and the properties of triangles and properties of angles (which can be seen in the sketch below) we are able to find the derivation for n. (Note: Joel stepped us through this process)
Derivation of n: Media:nderivation.pdf
Notes for Derivation: Beta is assumed to be 90 degrees and alpha is assumed to be 45 degrees because that is how the laser has been positioned. Gamma is the angle between the original, unrefracted beam and the final refracted beam. It is assumed that gamma can be found using the arctangent of the difference between the original beam and the refracted beam and the length between beta and where the beam hits the wall. This, though, is slightly wrong (unless the incidence angle is the minimum deviation, because only then is the imaginary triangle that can be made by extending the normal lines where the light beam hits the face of the aerogel is the angle gamma actually under beta). Due to the fact that you are measuring from the wall where the light hits to gamma, if the angle is not directly under it, the calculations will be slightly off. Finally, x is the distance between the unrestricted beam and the refracted beam and L is the distance from beta to the wall.
The refractive index can be found in the set up shown to the right.The aerogel is placed horizontally on a raised platform with one of its corners in the path of the laser which is 40 cm away. The laser is then turned on and passes through the aerogel. The light of both the original unobstructed beam and the refracted beam appear on the wall 108 cm away. The distance between the unobstructed laser and the refracted laser is then measure and put into a derivation to solve for n.
Aerogel SP-30 has a refractive index that ranges from 1.029 to 1.034. The SP-30 tiles' refractions are much more dispersed. There were a few outliers (one of which can be seen in the bottom figure on the right)that were removed from the data.The first oulier was slanted white the other outlier was very cloudy, but could not be seen in a picture. They were retested, but still remained the same. Both the histogram(Figure 1) and the scatter plot (Figure 2) of the data can be seen below.
Aerogel SP-20 has a refractive index between 1.018 and 1.023. The mean is 1.02 and the standard deviation is .0009. The scatter plot and histogram can be seen in Figures 3 and 4 below.
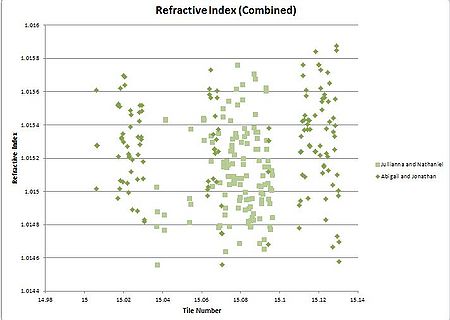
Aerogel SP-15 has a refractive index that ranges from 1.0146 to 1.0158 with a few outliers beyond that. (These outliers have been retested and have remained the same.) This can be seen in the scatter plot in Figure 5. When the refractive indices of the SP-15 tiles are put into a histogram they are centered around the mean 1.0152 and have a standard deviation of .00028. This can be seen in the histogram in Figure 6.
Uncertainty
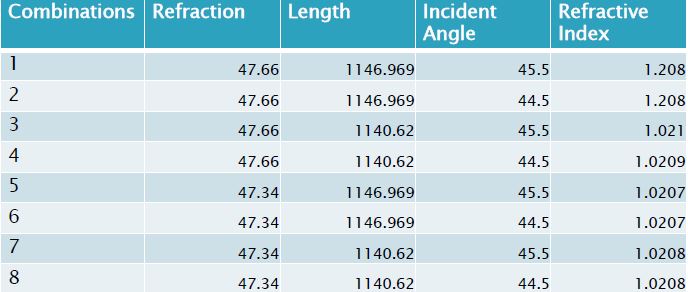
To calculate uncertainty, we measured the distance between the refracted and unrefracted beam through one tile ten times in a row and found that the measurements had a uncertainty (standard deviation) of .161 mm. We were given that the uncertainty for the distance between the aerogel and the measuring wall was 3.175 mm. Although the incident angle was set, we assumed that the angle could be 45 degrees +/- .5, and therefore made .5 our incident angle uncertainty. We then calculated the refractive index using all possible combinations of variable plus or minus their uncertainties.These cases can be seen in the chart below with the refractive index they produced. Once we had all of the refractive indices we took the highest and lowest values and found the difference between them. This value was our worst case uncertainty. The uncertainty may be high due to the fact that we are working with the worst case. Because we tested a SP-20 tile for this procedure, the results that we got only applied to the SP-20 tiles. In order to find the uncertainty for the SP-15 and SP-30 tiles, we took the uncertainty in the measurements between the refracted and unrefracted beams that we found before (on the assumption that because Jonathan measured the majority of the tiles, the error would not change) and applied it to the other sets of tiles.
Uncertainties:
SP-30: +/- .0002 SP-20: +/- .00015 SP-15: +/- .0001
Incident Angles
The angle the laser hits the aerogel effects how much the light will refract. Around 45 degrees (+/- 2 degrees) the incident angle is said to be approximately the minimum deviation angle (the angle at which light is deflected the least). With Joel's help we derived the relationship between the incident angle and the refraction distance assuming that the incident angle is the minimum deviation angle. The derivation is below:
Media:Indicent Angle Derivation.pdf
We then repeated the derivation under the condition that the laser beam goes directly through the tile entering from one side and exiting from the opposite end. Joel stepped us through the derivation and can be seen below.
Media:Straight Through Refractive Index.pdf
We then experimented with the scenario and found that the refraction of the beam is almost unnoticeable small. This is because the unrefracted beam is parallel to the refracted beam. When exiting from an adjacent side, the beams are not parallel. This allows us to increase L (the distance from the gel to the wall, and therefore increase x (the distance between the beams when they hit the wall).
Aerogel Thickness
The thickness of the SP-15 tiles are between 10 and 11 mm. The tiles have to be measured in order to correctly set the wires that will hold them in the detector at Jefferson lab. We used two different methods to test the thickness of the aerogel. First, we put the aerogel between two pieces of metal that were exactly 3 mm thick (Figure 7). Then, after putting the aerogel tile in-between the metal plates, we tested the thickness again (Figure 8). The aerogel's thickness was then the overall thickness minus the thickness of the metal. This way, though, was somewhat subjective depending on how hard we pushed on the caliper when measuring the tiles. Therefore, we changed out method while using the same set-up. Instead of measuring the outside of the metal we measured the inside. This method slightly reduced the subjectivity. The data fit with a Gaussian curve can be seen in Figure 9. The data is centered around the mean 10.43 and has a standard deviation of 0.24.
Jullianna tested the thickness of the SP-30 tiles before. To verify her data we tested two more tiles and they fell within her range of data (Figure 9). The two points are represented by arrows in the graph to the right. The combined graph of data fit with a Gaussian curve can be seen in Figure 10. The data is centered around the mean 11.36 and the standard deviation is .33.
Uncertainty
We believe that the systematic uncertainty in the measurements for the thickness is .01 mm. We applied this uncertainty to all of the individual points. We then calculated how many tiles each thickness bin would gain or lose if the uncertainty was added to each point. This can be seen in Figure 9. For Jullianna's data we did not add error bars because we did not have her original data but only the general points from Figure 9 that we added to to make Figure 10. We therefore were not able to calculate the uncertainty for her graph.
Humidity effects over Aerogel Tiles
Aerogel Detector, is how the aerogel will behave. We know from papers that it is manufactured by drying silica gel. So, in principle, the tiles can absorb water again and change their densities. As their densities are directly related to their refractive indexes, it is important to understand any change we may find. The tiles we have are coated by an hydrophobic thin layer of material, so we have a protection on them already. And the trays of the detector will be rightly stored. But studying the water absorption and its effects on the aerogel properties would be an interesting way of understanding better our detector.
The first idea would be to construct an isolated box to have one aerogel tile submitted for a long time into high humidity. From time to time, we would measure the mass and refractive index of the tile to see any change on its properties.
Materials we bought for the project:
- Humidifier - Honeywell HCM-630 Quietcare™ Cool Moisture Humidifier
- Humidifier controller - General Tools Digital Temperature and Humidity Monitor
- Humidity Gauges - Extech 445815 Humidity Meter and GSI Quality Handheld Pen-Shaped Hygro Thermometer
One of our concerns for the long term use of aerogel, in the Kaon * Plastic box to create the controlled environment (18x22x23 cm) - Snapware 40-cup
- Water-resistant clear polyurethane tubing, 1/2" inner diameter, 5/8" outer diameter, 1/16" wall thickness
Design of Humidifier:
We captured the output using a funnel and connected it to the plastic box using plastic tubing and tape. By punching small holes in the top of the box, we allow air to escape and prevent a build up of pressure within the chamber. We placed a humidity gauge within the chamber in order to monitor the percentage of humidity within the box.
Calibrating and Testing the Hygrometers:
To test the accuracy of the hygrometer we are using about a table spoon of salt, a few drops of water, and an air tight plastic bag. We begin by combining the salt and water in a bottle cap to make a salt slush (we do not want it to be dissolved). We then put the bottle cap into the bag, added the hygrometers, and sealed the bag. The hygrometer should read 75% relative humidity (RH) becuse "Salt does not absorb moisture until the humidity reaches 75 percent. Any absorbed moisture will evaporate when the humidity falls below 75 percent."(http://www.saltinstitute.org/Uses-benefits/Winter-road-safety/Salt-storage) Therefore, the salt will continue to release water until the RH reaches 75%.
Within our specific test we found that the GSI Quality Handheld Pen-Shaped Hygro Thermometer read 72% RH.
We then tested both humidity gauges with a damp paper towel wrapped around their sensor. The reading was suppose to be between 90 and 100% RH. For the GSI Quality Handheld Pen-Shaped Hygro Thermometer the reading was 95% RH and for the Extech 445815 Humidity Meter the reading was 99% RH. We believe that the difference here was that the paper towel on the Extech 445815 Humidity Meter was more moist than the one on the GSI Quality Handheld Pen-Shaped Hygro Thermometer and therefore received a higher reading.
When left in the lab both read 53% after 3 hours and when left in the humidifier on high for an hour the GSI Quality Handheld Pen-Shaped Hygro Thermometer read 78% RH and the Extech 445815 Humidity Meter read 80% RH.
Testing the Humidifier
We found that the humidifier produces a humidity of about 80% throughout the entire box. By placing the humidity detectors in different corners and under the tube, we found that the humidity did not change based on location in the box.
Testing the Tiles
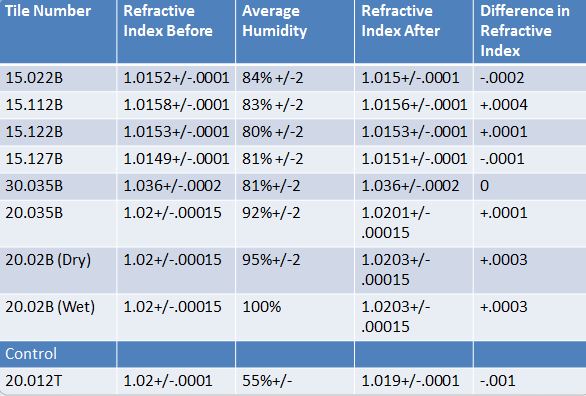
To test the affect of humidity on aerogel we ran 24 hour tests on tiles of aerogel within the humidifier. The highest setting for the humidifier was approximately 84%, so our first fie tests were run at this level of humidity. In order to raise the level of humidity for the following tests we added 100 ml to 150 ml of water to the bottom of the container for the aerogel and then put the aerogel on top of a stand. This raised the humidity to between 90% and 94% relative humidity. The last two tests were run with the 90% humidity. Overall we found that humidty, and even direct contact with water has little to no affect on the aerogel from ------. A chart of the results can be seen below.
Transmittance
The transmittance of a tile is how much light of different wavelengths can travel through the tile. Using a PerkinElmer Lambda 750 UV/VIS/NIR spectrometer, we tested the transmittance of SP-30 and SP-20 aerogel between 200nm and 900nm wave lengths. Two tiles were tested from each group, one with a normal refractive index and one with a high refractive index. The SP-30 were particularly scratched, but all four tiles had similar amounts of dust on them. Due to the fact that the SP-30 tiles are denser than the SP-20 tiles, we believed that they would have a higher refractive index. We also concluded that within the categories of the SP-30's and SP-20's the tile with the higher refractive index would have the lower transmittance. Once the tests were run, though, the results were the opposite of the expected outcome. Between the SP-30's and SP-20's, the SP-30's had higher transmittance; between the the tiles of the same refractive index, the one with the higher refractive index showed a higher transmittance.
When analyzing the collected data and re-evaluating the tiles, we found that the SP-20 tiles were considerably more cloudy than the SP-30's, and that one of the SP-30 tiles was considerably more cloudy than the other one. Although cloudiness would not necessarily affect the density of a tile, it would affect the transmittance more than the change in density between the SP-30 and SP-20 tiles. When calculating the density change between the SP-30 and SP-20 tiles, we found that the SP-30 tiles are approximately 34% denser than the SP-20 tiles. The difference between the transparency is very large, though, allowing it to be the dominant factor in the transmittance test. The information for the actual densities for the four tiles is off by a factor of 100, but this should not affect the percent difference between the densities of the two sets of tiles.
We then measured one tile four times without changing it to determine the consistency of the spectrometer. By comparing the values at each wavelength, we found that the standard deviation for the machine's measurements was .24 nm. The comparative data of the transmittance test can be seen in Figures 12 through 14. More graphs and analysis of the aerogel's transmittance can be seen here: Media:Aerogel Transmittance.pdf